Рекомендации:Порядок вывода комментариев: По умолчаниюСначала новыеСначала старые
|
Математическая шкатулка — Федор Нагибин
Загрузка. Пожалуйста, подождите…
Просмотров: 3654
Махинация (СИ)
Елена Звездная
Было забавно сидеть и смотреть на мегаполис с такой высоты… казалось ты здесь, высоко, над всеми…
Просмотров: 2966
Неласковый отбор для Золушки (СИ)
Светлана Волкова
Идешь домой с репетиции и попадаешься шайке гопников. Удрать в здание заброшенного завода – и…
Просмотров: 2954
Замужем по ошибке (СИ)
Вера Окишева
Татьяна никогда не верила в магию. Может, потому, что никогда с ней не сталкивалась, или просто…
Просмотров: 2613
Бракованная невеста (СИ)
Наталья Шульмайстер
Какая бы девушка не закатила истерику, узнай, что утром у нее свадьба? А жениха она в глаза не…
Просмотров: 2232
Любовь, как приговор или гаечный ключ для девушки не помеха (СИ)
Ирина Лисовская
Возможно ли счастье после предательства? Наверно, нет. Так думала наша героиня. А вот судьба решила…
Просмотров: 2177
Провинциалка 2. Дорога назад
Анастасия Шерр
Кто бы мог подумать, что я переживу изнасилование, избиение, постою на краю пропасти в преисподнюю……
Просмотров: 2164
его Детка (СИ)
Милау Элли
Скромница, провинциалка, неудачница? Только не с ним, с ним она совершенно другая…
Просмотров: 1858
Нянька для злодеев
Юлия Ханевская
После школы Лорелия решила поступать не в какой-то скучный вуз, а в академию Семи Магов. Почему бы…
Просмотров: 1812
Даже хорошие девочки делают это (СИ)
Жасмин Майер
Ася всегда была хорошей девочкой, но под Новый год она пришла на вечеринку с четкой целью –…
Просмотров: 1731
Стокгольмский синдром
Эмилия Грин
Эксцентричный миллиардер, который не верит в любовь, похитил девушку себе на потеху. Вот только он…
Просмотров: 1540
Без правил
Lina Mur
Говорят, первую любовь забыть невозможно. А если она была приправлена болью, разочарованием…
Просмотров: 1534
Мама из другого мира. Дела семейные и не только (СИ)
Ехидна Рыжая
Есть тайны, охраняемые лучше королевских сокровищниц, прошлое любит стучаться в дверь когда ты его…
Просмотров: 1468
Жеребец
Эмилия Грин
Эрик Уильямс самый популярный студент университета. О его выходках ходят легенды. Он вселяет…
Просмотров: 1397
Судьба-шутница
Марина Орлова
Я всего лишь хотела спокойной жизни для себя и сестры. Неужели я так много просила? Мы и так…
Просмотров: 1388
Подружка для зануды
Валентина Кострова
Они совершенно разные по темпераменту, по взглядам на жизнь. Говорят, что противоположности…
Просмотров: 1385
Этот жестокий волшебный мир — 2
Юлия Ханевская
Спустя множество бед и потерь, счастье особенно сладко – теперь Алесана сама сможет убедиться в…
Просмотров: 1362
Замуж за 30 дней (СИ)
Лючия фон Беренготт
Никогда и ни с кем не спорьте на пьяную голову! Особенно с вреднющей младшей сестрой, которая…
Просмотров: 1317
Провинциалка. Книга первая
Анастасия Шерр
«Москва слезам не верит» – вот главное правило, которое нужно знать наизусть, если решила приехать…
Просмотров: 1310
Черные вороны. Обрыв
Ульяна Соболева
Я больше ему не нужна. Мой муж исчез. Бросил меня, ребенка и просто уехал, оставив бумаги о…
Просмотров: 1075
Наложница семи рыцарей в академии суккубов (СИ)
Аморелия Флитт
Отправляясь на свидание вслепую, Светлана и представить не могла, что её жизнь круто поменяется.…
Просмотров: 1021
Укрощение клубной бабочки (СИ)
Светлана Багрянцева
Была спокойная жизнь, тихое, милое сердцу одиночество в собственной квартире, и вереница любовниц…
Просмотров: 1016
Тиран
Эмилия Грин
Что вы знаете о боли? Точно меньше меня, парня, который провел целый год в колонии для малолетних…
Просмотров: 992
Его Высочество Ректор (СИ)
Лючия фон Беренготт
Устроить вечеринку с рейвом в общежитии старинного английского колледжа? Легко! Рвануть в Лондон на…
Просмотров: 919
Наперекор инстинкту (СИ)
Ксения Власова
Миа всегда обходила стороной оборотней. Конечно, те уже давно не оборачиваются в волков и многих из…
Просмотров: 888
Девственница на двоих (ЛП)
Пенни Уайлдер
Никто не сказал мне, что студенческое общежитие было смешанного типа.И меня определенно не…
Просмотров: 823
Подыграй мне (СИ)
Что делать, если изменил любимый парень с лучшей подругой? Не знаю как вы, а лично я, буду мстить.…
Просмотров: 739
Урок анатомии (СИ)
Алекс Найт
Короткая зарисовка случайной встречи, которая будет иметь внезапные последствия. В тексте:…
Просмотров: 708
Ничей ее монстр (СИ)
Ульяна Соболева
Любить ЖУТКОГО монстра не просто страшно, любить монстра больно и смертельно опасно. Мой монстр…
itexts.net
Математическая шкатулка — Математика — Прочее
Загадочные свойства чисел
Суеверия, связанные с числами, пожалуй, одни из самых живучих и распространенных. Человек, не верящий ни в какие приметы, все-таки стукнет три раза по столу, «чтобы не сглазить», или трижды плюнет через плечо. Если у нас случается неприятность тринадцатого числа в понедельник, то мы быстро находим ей оправдание: чего хорошего ждать в такой день. Из-за страха перед числом 13 в Англии и США в некоторых гостиницах отсутствуют комнаты с номером 13, лифт не останавливается на 13-м этаже, потому что он в нумерации попросту пропущен; нет таких маршрутов городского транспорта, а на авиалиниях большинства зарубежных стран самолеты до недавнего времени не имели бортового номера 13. Спортсмены избегают ставить этот номер на своих футболках.
У многих людей есть «свое», то есть любимое, счастливое число, и они почти серьезно верят, что это число приносит им удачу.
Нынешние наши суеверия — это отголоски древних представлений о мистической силе чисел. В племенах, у которых счет ограничивался числами два или три (один, два; один, два, три), все, что было связано со счетом предметов, превосходящих два или три, было равносильно понятию «много» или «тьма». То, что не поддавалось счету, находилось как бы за пределами разума и было таинственным, наделялось сверхъестественными свойствами, считалось священным.
Суеверных взглядов на числа придерживались и ученые древности, оказавшие своими открытиями огромное влияние на развитие и становление современной науки. Так, Пифагор, знаменитый древнегреческий математик, живший в VI веке до нашей эры, придавал огромное значение магии чисел. Он утверждал, что числа лежат в основе всего существующего, что источником гармонии мира являются числовые соотношения, а мир построен на силе чисел. «Вещи — суть копии чисел, числа — начала вещей», — говорил Пифагор.
Приписывал загадочные свойства числам и другой математик Древней Греции — Никомах, живший в конце I века нашей эры. Он положил начало теории чисел, создал учение о простых, составных числах, о пропорциях. И в то же время был серьезно убежден, что единица — это разум, добро, гармония, счастье и в то же время материя, тьма, хаос. Она соединяет в себе четное с нечетным и женское с мужским. Два — начало неравенства, противоречия, оно есть мнение, ибо во мнении встречается истина с ложью. Три — это первое настоящее число, так как оно имеет начало, середину и конец, и поэтому оно есть число «совершенное».

Магические числа
Среди однозначных чисел мы не найдем ни одного «просто числа», которому не приписывались бы магические свойства. Но многие двузначные, да и вообще многозначные числа тоже не обошла эта участь. Например, пятидесятница — Троица отмечается на 50-й день после Пасхи; семьдесят входит в понятие «Септуагинта» — древнейший перевод Ветхого завета на греческий язык.
У индусов была (воспринятая от халдеев) «особая любовь» к очень большим числам: в мифологии индусов говорится о существовании 24000 биллионов богов; Будда имел 600000 миллионов сыновей и мог перечислить все числа от 1 до 1054, то есть числа с 54 нулями.
Не только знание магических чисел, но и стремление вывести, рассчитать какое-то судьбоносное число (конец мира, например) было распространено в прежние времена, да и сейчас «кормит» астрологию и нумерологию.
Особое значение придается тайне дня рождения и тайне имени. Для этого составлены таблицы, где каждой букве имени и дню рождения соответствует определенное число. Сумма, полученная в результате сложения этих чисел, переводится в однозначное число от 1 до 9, которое и считается сущностью имени. То есть ему «соответствуют» какие-то свойства характера и им определяется судьба человека.
Конечно, ни гороскопы, ни тайны дня рождения и имени, ни злополучные числа три, семь и другие не могут оказать влияния на судьбу, характер и деятельность человека, верящего в свои способности. Но эти и подобные факторы у суеверного человека создают дополнительные эмоции, которые в одном случае прибавляют ему энергии и силы, придают большую уверенность в достижении поставленной цели, приносят некоторую радость, но в другом — подавляют волю, вызывают чувство страха, боязни, неуверенности и бесполезности борьбы с жизненными невзгодами. Широкая реклама астрологических прогнозов, услуг всяческих колдунов, чародеев, гадалок создает благодатную почву для «выращивания» суеверий.

Здесь спряталась поговорка
Задание непростое: сначала надо расшифровать загадку (читай слева направо сначала верхнюю строчку, затем — среднюю, затем — нижнюю). А потом отгадать эту загадку.
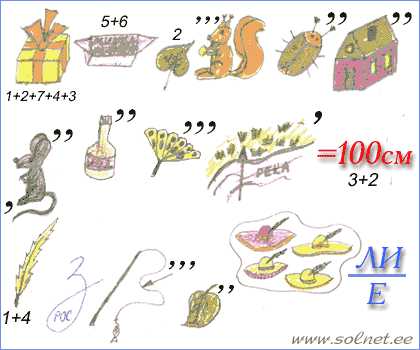

1. Чтоб одеть тепло сыночков, Не хватает двух носочков. Сколько же в семье сынков, Если в доме шесть носков? (оревтеч) | 2. Столько книжек у ребяток, Сколько у Алеши пяток. Принесла ребяткам Галя Мячик, книжку, мишек. Вы, ребята, посчитали, Сколько стало книжек? (ирт) | ||
3. К трем лягушкам у болота Прибежали два енота, Прискакала тетя жаба И пришла наседка Ряба. Сколько в камышах болотных Оказалось земноводных? (оревтеч) | 4. Я к реке иду из дома, А навстречу — сто знакомых. Вдруг один из ста ребят, Тот, что был с сачком в руке, Повернуть решил назад. Сколько нас идет к реке? (еовд) | ||
5. В нашей группе есть Антоша, Нина, Коля и Алеша, Витя, Ира, Вова, Маша, Соня, Кира и Наташа, Две Марины, Света, Миша. Сколько же всего детишек? (ьтацдантяп) | 6. Света принесла из школы Три пятерки за глаголы, За предлоги — тройку, А за суффикс — двойку. Сколько в дневнике у Светы Положительных отметок? (ерытеч) | ||
Математика и литература не так далеки друг от друга, как многие думают. Искусство и наука требуют фантазии, творческой смелости, зоркости в наблюдении различных явлений жизни. Служение математике С.В.Ковалевская представляла себе неотрывным от служения литературе.
«Мне кажется, — говорила она, — что поэт должен видеть то, чего не видят другие, видеть глубже других. И это должен математик».
Для многих казалось странным, как она сочетает математику с поэзией. По этому поводу Ковалевская писала: «Многие, которым никогда не представлялось случая более глубоко узнать математику, считают её наукой сухой. В сущности же это наука, требующая наиболее фантазии, и один из первых математиков нашего времени говорит совершенно верно, что нельзя быть математиком, не будучи в то же время и поэтом в душе».
Е сли ты в жизни, хотя на мгновенье
сли ты в жизни, хотя на мгновенье
Истину в сердце своём ощутил,
Если луч правды сквозь мрак и сомненье
Ярким сияньем твой путь озарил:
Чтобы в решеньи своём неизменном
Рок ни назначил тебе впереди —
Память об этом мгновеньи священном
Вечно храни, как святыню, в груди
Тучи сберутся громадой нестройной,
Небо покроется чёрною мглой,
С ясной решимостью, и с верной спокойной
Бурю ты встреть и померься с грозой.
Это стихотворение принадлежит выдающемуся учёному-математику Софье Васильевне Ковалевской. В ней одновременно жили математик и поэт. Они одновременно родились, росли, учились, писали научные труды и стихи.
Великий русский поэт М.Ю.Лермонтов был большим любителем математики и в своих вольных и невольных переездах из одного места службы в другое всегда возил с собою учебник математики.
Английский писатель XIX века Льюис Кэрролл, он же — Чарльз Лутвидж Доджсон, автор «Алисы в стране Чудес» и он к тому же был ещё профессор математики.


multiurok.ru
В БЛОГАХ… еще… КОММЕНТАРИИ еще… отучил говорить тот еге, попробуйте фарш обратно провернуть! а вскоре эти начнут… Ольга Куприяновна, приятно Ваше внимание и оценка моего материала, как опытного … Дорогие мои коллеги, спасибо вам за доброту и участие! Очень приятно ваше вниман… Хорошо, что связь не прерываете. Молодцы. Хороший материал. Взял для себя, проведу классный час со своими. Благо дарю! Лидия Петровна, я рада, что материал востребован коллегами! Большое спасибо за о… Ольга Викторовна, благодарю за полезный ресурс! |
| ||||||||||||||||||||||||
easyen.ru
В БЛОГАХ… еще… КОММЕНТАРИИ еще… отучил говорить тот еге, попробуйте фарш обратно провернуть! а вскоре эти начнут… Ольга Куприяновна, приятно Ваше внимание и оценка моего материала, как опытного … Дорогие мои коллеги, спасибо вам за доброту и участие! Очень приятно ваше вниман… Хорошо, что связь не прерываете. Молодцы. Хороший материал. Взял для себя, проведу классный час со своими. Благо дарю! Лидия Петровна, я рада, что материал востребован коллегами! Большое спасибо за о… Ольга Викторовна, благодарю за полезный ресурс! |
| ||||||||||||||||||||||||||||||||||||
easyen.ru
В БЛОГАХ… еще… КОММЕНТАРИИ еще… отучил говорить тот еге, попробуйте фарш обратно провернуть! а вскоре эти начнут… Ольга Куприяновна, приятно Ваше внимание и оценка моего материала, как опытного … Дорогие мои коллеги, спасибо вам за доброту и участие! Очень приятно ваше вниман… Хорошо, что связь не прерываете. Молодцы. Хороший материал. Взял для себя, проведу классный час со своими. Благо дарю! Лидия Петровна, я рада, что материал востребован коллегами! Большое спасибо за о… Ольга Викторовна, благодарю за полезный ресурс! |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
easyen.ru
Персональный сайт учителя математики — Математическая шкатулка
Математическая шкатулка

Абель Нильс Хенрих /abel_nils_khenrikh.rar
Евклид /evklid.ppt
Архимед /arkhimed.ppt
Франсуа Виет. Газета /gazeta-viet.doc
Николай Иванович Лабочевский /nikolaj_ivanovich_lobachevskij.ppt
Пифагор /pifagor.ppt
Портреты математиков /portrety_matematikov.ppt
Улукбек /ulugbek1.doc
Франсуа Виет. Презентация. /fransua_viet.ppt
Числа /chisla.ppt

Математика Древнего Египта.
Древнейшие древнеегипетские математические тексты относятся к началу II тысячелетия до н. э. Математика тогда использовалась в астрономии, мореплавании, землемерии, при строительстве зданий, плотин, каналов и военных укреплений. Денежных расчётов, как и самих денег, в Египте не было. Египтяне писали на папирусе, который сохраняется плохо, и поэтому наши знания о математике Египта существенно меньше, чем о математике Вавилона или Греции. Вероятно, она была развита лучше, чем можно представить, исходя из дошедших до нас документов — известно, что греческие математики учились у египтян.
Древнеегипетская нумерация, то есть запись чисел, была похожа на римскую: поначалу были отдельные значки для 1, 10, 100, … 10 000 000, сочетавшиеся аддитивно (складываясь). Египтяне писали справа налево, и младшие разряды числа записывались первыми, так что в конечном счёте порядок цифр соответствовал нашему. В иератическом письме уже есть отдельные обозначения для цифр 1-9 и сокращённые значки для разных десятков, сотен и тысяч.
Любое число в Древнем Египте можно было записать двумя способами: словами и цифрами.
Знание древнеегипетской математики основано главным образом на двух папирусах.
Материалы, содержащиеся в папирусах, позволяют утверждать, что за 20 веков до нашей эры в Египте начали складываться элементы математики как науки. Однако материалов, которые позволяли бы судить о развитии математики в Египте, ещё недостаточно.
Египтяне, числа первого десятка записывали соответствующим количеством палочек. А «десять» обозначалось скобочкой в виде подковы. Чтобы написать 15, надо было ставить 5 палочек и 1 подкову. И так до сотни. Для сотни придуман был крючок, для тысячи — значок вроде цветка. Десять тысяч обозначали рисунком пальца, сто тысяч — лягушкой, а миллион — знакомой нам фигуркой с поднятыми руками.
Не очень-то удобно было записывать таким способом большие числа и совсем неудобно было их складывать, вычитать, умножать, делить. Последовательно комбинируя эти символы, можно было записать любое число.
С появлением папируса возникла новая числовая система.
Математика Древнего Вавилона.
В древнем Вавилоне зарождение математики произошло задолго до нашей эры. Вавилонские памятники из глиняных плиток с древними клинописными надписями хранят музеи разных стран мира, в том числе они есть в Эрмитаже и московском музее изобразительных искусств. Найдены сорок четыре глиняные таблицы. В этих надписях можно узнать тексты ряда интересных задач, связанных со строительством, торговлей и земледелием. Всего найдены в общей сложности сорок четыре глиняные таблицы – своего рода древняя математическая энциклопедия вавилонян.
Вавилоняне писали клинописными значками на глиняных табличках, которые в немалом количестве дошли до наших дней (более 500000, из них около 400 связаны с математикой). Поэтому мы имеем довольно полное представление о математических достижениях учёных Вавилонского государства. Отметим, что корни культуры вавилонян были в значительной степени унаследованы от шумеров — клинописное письмо, счётная методика.
Вавилонские математические тексты носят преимущественно учебный характер. Из них видно, что вавилонская расчётная техника была намного совершеннее египетской, а круг решаемых задач существенно шире. Есть задачи на решение уравнений второй степени, геометрические прогрессии. При решении применялись пропорции, средние арифметические, проценты. Методы работы с прогрессиями были глубже, чем у египтян. Линейные и квадратные уравнения решались ещё в эпоху Хаммурапи; при этом использовалась геометрическая терминология. Многие значки для одночленов были шумерскими, из чего можно сделать вывод о древности этих алгоритмов; эти значки употреблялись, как буквенные обозначения неизвестных в нашей алгебре. Встречаются также кубические уравнения и системы линейных уравнений. Венцом планиметрии была теорема Пифагора.
Как и в египетских текстах, излагается только алгоритм решения (на конкретных примерах), без комментариев и доказательств. Однако анализ алгоритмов показывает, что общая математическая теория у вавилонян несомненно была.
Шумеры и вавилоняне использовали 60-ричную позиционную систему счисления, увековеченную в нашем делении круга на 360°, часа на 60 минут и минуты на 60 секунд. Писали они, как и мы, слева направо.
Впервые появляется (ещё при Хаммурапи) теорема Пифагора, причём в общем виде; она снабжалась особыми таблицами и широко применялась при решении разных задач. Вавилоняне умели вычислять площади правильных многоугольников; видимо, им был знаком принцип подобия. Для площади неправильных четырёхугольников использовалась та же приближённая формула, что и в Египте.
В вавилонской математике был осуществлён принцип, согласно которому одна и та же цифра имеет различную числовую значимость в зависимости от места, занимаемого ею в числовом контексте — позиционная система.
Всё же богатая теоретическая основа математики Вавилона не имела целостного характера и сводилась к набору разрозненных приёмов, лишённых доказательной базы. Систематический доказательный подход в математике появился только у греков.
Гораздо лучше придумали запись чисел в древнем Вавилоне. Она очень похожа на современную, только мы считаем десятками, сотнями, тысячами и так далее, а жители древнего Вавилона объединяли единицы по 60, по 3600, по 216000 и так далее. При раскопках были найдены целые библиотеки и архивы из таких табличек.
Палочкой на глине трудно изображать сложные фигуры, поэтому вавилонская письменность состояла, в основном, из различных комбинаций клинышков (ее так и называют — клинопись). Единицы изображались узкими вертикальными клинышками, а десятки — широкими горизонтальными, все числа до 60 «собирали» из таких клинышков. Когда надо было записать число, большее, чем 60, то открывали следующий разряд — в него писали, сколько раз число 60 помещается в записываемом числе, а то, что оставалось (то есть остаток от деления на 60), записывали, как и раньше, в первый разряд. Между разрядами оставляли пробелы, чтобы цифры из разных разрядов не смешивались.
Следы этой нумерации остались в исчислении времени, измерении градусной меры углов.
Математика Древней Индии.
Научные достижения индийской математики широки и многообразны. В древние времена учёные Индии на своём пути развития достигли высокого уровня математических знаний. Они изобрели десятичную систему записи чисел, предложили символы для 10 цифр. Развитие индийской математики началось, достаточно давно.
В Индии изобрели десятичную систему записи чисел. В новой системе выполнение действий оказалось проще, чем в старых, с неуклюжими буквенными кодами, как у греков, или шестидесятеричных, как у вавилонян.
Очень скоро потребовалось введение нового числа — нуля. Учёные расходятся во мнениях, откуда в Индию пришла эта идея — от греков, из Китая или индийцы изобрели этот важный символ самостоятельно. Первый код нуля обнаружен в записи от 876 г. н. э., он имеет вид привычного нам кружочка.
Дроби в Индии записывались вертикально, как делаем и мы, только вместо черты дроби их заключали в рамку. Действия с дробями ничем не отличались от современных.
Индийцы использовали счётные доски, приспособленные к записи.
Математика Древнего Китая.
Первые дошедшие до нас китайские письменные памятники относятся к эпохе Шан.
На гадальных костях найденных в Хэнани, сохранились обозначения цифр. Но подлинный расцвет науки начался после того, как в XII в. до н. э. Китай был завоёван кочевниками Чжоу. В эти годы возникают и достигают удивительных высот китайская математика. Появились первые точные календари и учебники математики. «Истребление книг» императором Цинь Ши Хуаном не позволило ранним книгам дойти до нас, однако они, скорее всего, легли в основу последующих трудов.
Цифры обозначались специальными иероглифами, которые появились во II тысячелетии до н. э., и начертание их окончательно установилось к III в. до н. э. Эти иероглифы применяются и в настоящее время. Например, запись числа 1946, используя вместо иероглифов римские цифры, можно условно представить как 1М9С4Х6. Однако на практике расчёты выполнялись на счётной доске суаньпань, где запись чисел была иной, как в Индии. В отличие от вавилонян — десятичной.
Китайская счётная доска по своей конструкции аналогична русским счётам. Нуль сначала обозначался пустым местом, специальный иероглиф появился около XII века н. э. Для запоминания таблицы умножения существовала специальная песня, которую ученики заучивали наизусть.
Престиж математики в Китае был высок. Каждый чиновник, чтобы получить назначение на пост, сдавал, помимо прочих, и экзамен по математике, где обязан был показать умение решать задачи из классических сборников. Наиболее содержательное математическое сочинение Древнего Китая — «Математика в девяти книгах».
Математика в Древней Греции.
Вплоть до VI века до н. э. греческая математика ничем не выделялась. Были, как обычно, освоены счёт и измерение. Греческая нумерация (запись чисел), как позже римская, была аддитивной, то есть числовые значения цифр складывались. Первый её вариант (аттическая, или геродианова) содержали буквенные значки для 1, 5, 10, 50, 100 и 1000. Соответственно была устроена и счётная доска (абак) с камешками. Кстати, термин калькуляция (вычисление) происходит от «calculus» — камешек. Особый дырявый камешек обозначал нуль.
Позднее (начиная с V века до н. э.) вместо аттической нумерации была принята алфавитная — первые 9 букв греческого алфавита обозначали цифры от 1 до 9, следующие 9 букв — десятки, остальные — сотни. Чтобы не спутать числа и буквы, над числами рисовали чёрточку. Числа, больше 1000, записывали позиционно, помечая дополнительные разряды специальным штрихом (внизу слева). Специальные пометки позволяли изображать и числа, больше 10000.
kolesnikovalud.ru