Чем отличается круг от шара?
Школьные годы для большого количества взрослых – синоним беззаботной поры детства. Вполне понятно, почему многие дети и подростки не горят желанием каждый день ходить в школу – но именно в ее стенах они получают общие знания о мире и навыки социальной жизни, которые становятся незаменимыми после получения аттестата зрелости.
Одним из таких вопросов, таких общих понятий является тема сходств и различий круга и шара. Спутать рассматриваемые понятия одновременно просто и сложно – потому что различий между кругом и шаром не так много, как кажется малоопытному ребенку.
Итак, в чем же несходства между шаром и кругом? Чем они похожи?
Что такое круг?
Начертание круга начинается с окружности. Окружность – это замкнутая черта без конца и начала, каждая точка которой находится на равном удалении от центра. Простейший пример окружности – гимнастический обруч.

Окружность
Круг получится, если начертить окружность, например, на бумаге – и потом разукрасить ее. Любыми красками: желтой, синей, зеленой – какая больше нравится. Главное – заполнить чем-то пустоту. После окончания работы окружность превратится в фигуру, которую именуют кругом. Круг по сути своей – это некоторая часть двухмерной поверхности, закольцованная в окружность.

Круг
Круг обладает некоторыми важными для понимания его сущности параметрами. Кстати, часть данных параметров присуща и окружности.
- Радиус – расстояние от центральной точки круга или окружности до границы фигуры (линии, которая ее очерчивает).
- Диаметр – важная характеристика, которая так часто фигурирует в школьных заданиях. Это сумма двух радиусом, то есть расстояние между двумя противоположными точками на окружности.
- Площадь – свойство, характерное только для круга. Окружность не имеет его в силу своей структуры (потому что она пустая, а центр фигуры – воображаемая точка). В круге, напротив, несложно определить центр. Через центральную точку фигуры достаточно просто прочертить ряд линий, которые поделят круг на сектора.
Круг в реальной жизни
В реальности можно без особых усилий отыскать множество предметов, по форме тождественных кругу. К примеру, готовый образец круга – а, точнее, множество, — каждый день катается по дорогам поселков и городов. Понятно, что речь идет о колесе. Здесь стоит оговориться: круг не должен быть однотонным, это не обязательно. Он может быть украшен узорами или чем-то еще – от этого форма не изменяется.

Колесо
Другой пример круга – Солнце. Да, то самое дневное светило, которое люди лицезреют каждый день. Любознательный читатель заметит, что Солнце – фигура объемная, она не может быть кругом. Это правда. Но маленькая фигура, какой предстает огненная звезда жителям Земли – по сути своей именно круг. Площадь его, конечно, высчитать не получится. Почему? Потому что этот пример приводится только для наглядности, для того, чтобы понять, что такое круг.

Солнце
Сектор
Что такое круг внимательный читатель ужен разобрался. Но вот что за «зверь» этот сектор, о котором упоминалось немного выше? Сектор – это часть круга, отделенная от остальной поверхности парой начерченных радиусов. Для наглядности можно примести такой пример: все когда-нибудь видели нарезанную пиццу. Кусочки – это сектора круга, которым является все это аппетитное блюдо.
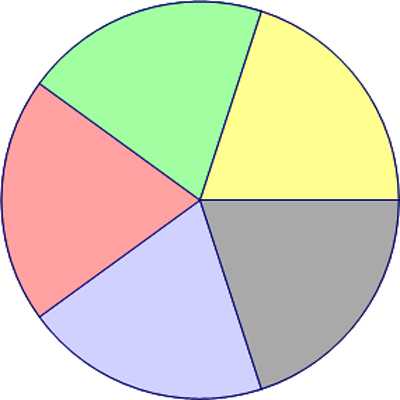
Сектора круга
Секторы не обязательно должны быть равной величины. К примеру, если пицца разрезана пополам, обе ее половины тоже будут секторами круга.
Что такое шар?
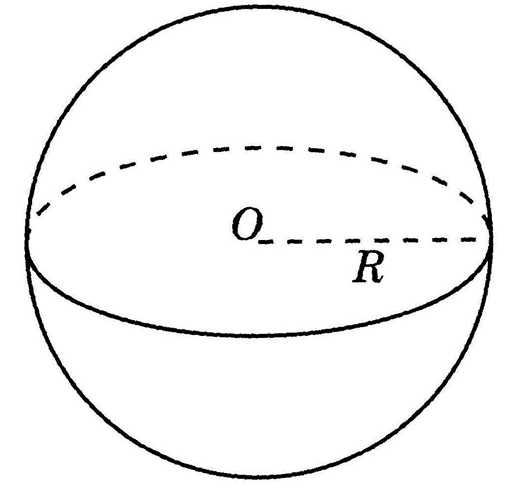
Шар – тело, ограниченное сферической поверхностью. То есть, это не двухмерная фигура, как круг, а трехмерная. Сферическая поверхность – это геометрическое сочетание поверхности точек, расположенных на неотрицательном расстоянии от некоей центральной точки. Расстояние, на которое удалены все точки поверхности шара от его центра, называется радиусом. И оно не должно превышать некие заданные цифры. Таким образом, круг – это та же сферическая поверхность, расположенная в другом пространстве.

Шар
В этом проявляются сходства и главное различие шара и круга. Круг – это двухмерная фигура, точки которой ограничены окружностью. Шар – это фигура трехмерная, а ее точки ограничены сферической поверхностью.
Разновидности шара
В метрическом и векторном пространствах рассматриваются два понятия, имеющие связь со сферической поверхностью. Шар, который включает в себя данную сферу, именуют замкнутым. Шар, который не включает в себя сферу, называют открытым.
Характеристики шара
Шар, как и круг, имеет диаметр и радиус. Обе эти величины в шаре вычисляются по вышеописанным принципам (как для круга). Радиус шара – это отрезок между любой точкой на сферической поверхности, ограничивающей фигуру, и ее центром. Диаметр соединяет две точки на сферической поверхности шара, проходя через его центр.
Интересное дополнение: круг может быть частью шара. Точнее, шар состоит из очень большого количества кругов различного диаметра. Называются эти круги сечениями сферы. Когда сечение пролегает через центр шара, его именуют большим кругом. Все остальные сечения именуются малыми кругами. Такого рода сечений, проходящих через пару точек на поверхности шара, возможно начертить поистине бесконечное множество.
Выводы
Круг – плоская, двухмерная фигура. Шар – объемное трехмерное геометрическое тело. Тем не менее, они имеют массу сходств (наличие ограничивающей поверхности, диметра и радиуса, наполненность структуры в отличие от той же окружности, возможност вычислить площадь).
Чем же отличается круг от шара? Круг плоский, шар же имеет объем. Именно объемность шара позволяет ему делиться на сечения, которые по своей сути являются кругами. Круг, напротив, делится на сектора.
vchemraznica.ru
Круг, окружность, шар. 6-й класс
Разделы: Математика
Цели урока:
Обучающая: выведение формулы длины окружности и площади круга, знакомство с числом п, обучение применению формула при решение задач.
Развивающая: развитие кругозора, мышления, внимания, культуры математической речи, привитие интереса к изучению математики.
Воспитательная: воспитание ответственности, аккуратности и самостоятельности.
Подготовка к уроку:
— прочитать “Вий” Н.В. Гоголя;
— пофантазировать, что мы можем увидеть в геометрической фигуре (голова клоуна; золотую рыбку и т.д.)
— на доске начертить окружность диаметром 1 м.
На учебной доске: Окружность, круг, шар (рисунок).
Рисунок 1 (Приложение)
Это я знаю и помню прекрасно.
Пи – лишние знаки тут чужды, напрасны.
3,14
Учитель: Сегодня мы с вами являемся сотрудниками научно исследовательского института, и к нам в институт пришло много писем, но письма необычные.
Письмо 1
— Задумал змеиный царь, а потом снял кольцо с руки и отдал Семёну и сказал ему потихоньку на ухо, как надо действовать с кольцом, чтобы вызывать волшебную силу.
“Волшебное кольцо”
Так Семён интересуется, какой диаметр кольца, которое обладает такой силой.
Учащиеся: Кольцо имеет форму окружности (окружность геометрическая фигура все точки которой лежат в одной плоскости и находятся на одинаковом расстоянии от центра). Учащиеся измеряют диаметр кольца с помощью штанген-циркуля (d=1,7 см)
Окружность имеет центр, а отрезок, соединяющий центр с какой-либо точкой окружности, — радиусом. Все радиусы имеют одну и туже длину.
Отрезок, соединяющий две точки окружности, называется её хордой. Хорда, проходящая через центр окружности, называется диаметром. Радиус и диаметр связаны формулой:
C=П*d, что такое d=2r.
Длина окружности равна произведению числа П на диаметр окружности:
С= 3,14* 1,7 см.
П
Оказывается уже древние греки использовали П для решения задач на практике П3. Довольно точное значение числа П в третьем веке до н.э. нашёл древнегреческий учёный Архимед П3,14 это приблизительное значение. Но оказывается число П можно использовать с точностью до 12 знаков, если вы запомните двустишие (записано на доске).
— Но уважаемые сотрудники вам было дано домашнее задание от садовника, несмотря на холод на улице вы должны были 13 саженцев рассадить на небольшой участок земли так, чтобы в ряду было по три саженца.
Рисунок 2 (Приложение)
— Что вы ещё можете рассказать об окружности.
Письмо 2
“- Ах, ужасно плохо я спала!
— пишет принцесса — я всю ночь не сомкнула глаза. Бог знает, что там у меня было в постели! Я лежала на чём-то твердом и теперь у меня всё тело в синяках! Это просто ужас что такое!”.
— От кого пришло письмо?
— От принцессы из сказки “Принцесса на горошине”.
— Принцесса интересуется — на чём она спала, и каких размеров был этот предмет?
Горошину измеряют — штангенциркулем.
Письмо от “Барона Мюнхгаузена”
“- Я стоял рядом с огромной пушкой, которая полила по турецкому городу, и когда из пушки вылетело ядро, вскочил на него и понёсся вперёд. Все в один голос воскликнули
— Браво, браво барон!”.
Барон интересуется, какой формы был этот предмет?
— Какую форму имело ядро у барона?
— Форму шара. (Поверхность шара – кривая поверхность, она называется сферой. Все точки сферы удалены от центра шара на одинаковое расстояние. Отрезок, который соединяет любую точку сферы с центром шара, называется радиусом шара).
Здесь учащиеся показывают своё домашнее задание “фантазия – шар”.
Письмо от колобока
Просит старик:
— испеки мне, старая, колобок.
Я колобок, колобок!
По амбару метён
По сумкам скребён,
На сметане сажён
На окошке стужён
Я от дедушки ушёл
Я от бабушки ушёл.
Колобок спрашивает, когда его разрезали на две половины, то бабушка с дедушкой удивились, у них получилось сечение шара плоскостью круг.
Найдем площадь круга радиусом равным 10 см.
Найдём S кр= П*r?
Учитель: У нас на доске окружность d= 1м. Так, приблизительно выглядит цветок с интересным названием раффлезия. Найдите площадь цветка.
— Найдем радиус r=0.5м.
— Что такое раффлезия?
— Его цветы одни, из самых больших в мире. У раффлезии Туан-муде их диаметр достигает 1 м, у раффлезии Арнольда 45 см. Они появляются на корнях других растений, это растение – паразит. Встречается в северо-восточной Индии, в Индокитае, на Филиппинских островах. От прорастания семян до появления бутона проходит три года. Ещё полтора года нужно для того, чтобы бутон раскрывался и превратился в цветок. Удивительно, что этот цветок живёт очень мало от 2 до 4 суток.
Цветки раффлезии появляются не часто.
Их находят в трудно-доступных местах, там, где почва обильно удобрена помётом слонов.
— А какой силой обладает окружность?
— Повесть Н.В. Гоголя “Вий” (домашнее задание прочитать “Вий”). “….Она идет прямо к нему. В страхе очертил он около себя круг. Наконец гроб вдруг сорвался со своего места …философ видел его почти над головою, но вместе с тем видел, что он не мог зацепить круга.
Письмо 5
От редакции журнала “Очевидное-невероятное”. Найти площадь выделенной фигуры?
Рисунок 3 (Приложение)
S выделенной фигуры =?
Решение:
Sкв.- Sкр.=а2—Пr2=42-3,14*22=3,44 см?
— Внимание чёрный ящик!
Этот ящик нам прислали археологи, они сообщают, что:
— Самый древний этот предмет пролежал в земле 2000 лет.
За многие сотни лет конструкции этого предмета практические не изменилось, настолько была она совершена.
— В Древней Греции умели пользоваться этим предметом, считалось верхом совершенства умение решать задачи с его помощью – признаком высокого положения в общества и его большого ума.
— Об этом предмете придумана загадка.
“Сговорились две ноги, Делать дуги и круги”. (Циркуль)
Письмо 6. Письмо от художников
Оказывается, художники, прежде чем, что-то нарисовать занимаются простым геометрическим построение м, разбивая на геометрические формы данный предмет. (На урок приносим живого кота, желательно пушистого; учащимся предлагаем рассмотреть кота сточки зрения геометрических фигур).
И учащиеся определяют, что кот состоит из трёх шаров, а шар на плоскости будет иметь форму окружности.
Сейчас я вам докажу, что вы все великие художники.
Построение: построим квадрат со стороной 10 см, проведём диагональ, на которой и будут находиться центры всех трёх окружностей. Строим большую окружность, чтобы она касалась прямого угла квадрата; следующая окружность – средняя; заканчиваем маленькой окружностью, которая касается сторон угла квадрата. Заканчиваем: мордочку, лапки и хвост
Рисунок 4 (Приложение)
- Сначала чертим квадратную рамку. Проводим в ней диагональ. Примерно в середине диагонали ставим т.А. Из этой точки проводим окружность. Затем из точки Б проводим вторую окружность, вернее её часть, и 0, наконец, из точки В – часть трет. Окружности. Основа будущего рисунка уже есть.
- Рисуем усы, лапки, хвост из т. А проводим полуокружность для улыбки стираем ластиком диагональ вместе со всеми точками, они нам больше не понадобятся.
- Рисуем глаза, носик и линию, которая соединяет нос со ртом.
- Убираем ластиком лишние линий. Рисуем усы и раскрашиваем рисунок как кому нравиться.
Всё!
Окр (А; 2) если квадр. 9*9 см
От А 1,2 см пол. Б и окр. (Б; 2,5)
АБ=БВ
Окр. (В; 3 см)
Окр. (А; 0,7 см) полуокружность для улыбки.
Стираем диагональ и другие дополнительные линии.
А теперь посмотрите друг другу в глаза и обратите внимания, что радужная оболочка имеет форму круга, а круг в математике считается фигурой доброй, и глаза у нас с вами добрые и веселые.
Рефлексия.
На этом наш урок закончен, всем спасибо.
Отметись самых активных.
Домашнее задание: Найдите площадь выделенной фигуры.
Рисунок 5 (Приложение)
18.11.2010
xn--i1abbnckbmcl9fb.xn--p1ai
Тема: Шар и круг
Занятие по математике(пространственная геометрия)
в предшкольной группе
Тема: Шар и круг
Задачи: формировать умения различать круг и шар; развивать мелкую моторику рук и пальцев; быстро отвечать, аккуратно закрашивать, воспитывать внимание, усидчивость.
Материал: мячи, бумажные круги, цветные карандаши, пластилиновые шары, стеки.
Методы и приемы: художественное слово, объяснение, показ, тактильное упражнение, творческое задание.
Ход занятия
Воспитатель:
Футболисту, футболисту,
Зной и ветер нипочем!
Дождь не страшен футболисту,
Если дружит он с ……..(мячом)
Предлагаю вам пройти лабиринт и помочь футболисту на рисунке забить в ворота гол (индивидуальная работа)
Воспитатель: посмотрите и сравните между собой.
Показывает несколько мячей- Футбольный, резиновый, легкий, надувной.
-Что в них общего?
-Чем они отличаются?
Воспитатель предлагает выбрать какой-нибудь мяч и составить о нем маленький рассказ.
Воспитатель раздает пластилиновые шары.
Дети вспоминают, что шар можно «обнять» ладонью и пальцами рук. Это объемное тело.
Воспитатель предлагает стеком разрезать шар на две одинаковые половинки.
Какая фигура у вас получилось?
Шар прячет внутри себя круг.
Круг – это геометрическая фигура.
Называют меня круг
Солнцу я отличный друг
С ним во многом мы похожи:
Солнце круглое, я -тоже
Много у меня друзей
Ты найди их поскорей.
На листе бумаги дети с помощью трафарета рисуют круг, закрашивают его и вырезают ножницами.
Тактильное упражнение:
Воспитатель предлагает детям положить вырезанный бумажный круг между ладонями и плотно их сжать. Пальцы и кисти рук при этом совершенно прямые. Если круг не очень большой, можно даже не догадаться, что между ладонями что-то спрятано, потому что круг плоская фигура.
Игра «Шарообразное – не шарообразное»
Игра напоминает игру «Съедобное — не съедобное». Дети становятся в круг. В руках ведущего мяч. Ведущий называет какой0нибудь предмет и, быстро поворачиваясь внутри круга, кидает мяч любому из игроков. Игрок ловит мяч и возвращает его со словами «шарообразное(ая, ый) или не «шарообразное»
Творческое задание
С помощью трафарета на листе бумаги нарисовать круг, а потом превратить его в какой-нибудь предмет или существо.
предлагает послушать стихотворение о шаре:
Воздушный шарик надуваю
Его, как мячик я кидаю,
На форму я его смотрю.
Он круглый, как и плоский круг
Но кругу он объемный друг.
Такой же формы апельсин,
Арбуз, и мяч, и мандарин.
Фигуру, что могу катать
Я буду шаром называть.
Физкультминутка:
Вот веселый клоун Бом
(прыжки на месте)
Клоунский колпак на нем
(хлопки в ладоши)
Разноцветная рубашка
(прыжки на месте)
И штанишки на подтяжках
(хлопки в ладоши)
А в руке большой, воздушный
шарик непослушный
(руки медленно поднимаются вверх)
Бьется шарик как живой……
(качают руками над головой)
Улетает! Ой-ё, ёй!
(бросить руки вверх потом вниз)
Раз, два, три, четыре, пять!
Шарик больше не поймать!
(хлопки в ладоши)
II часть. Работа в тетрадях на печатной основе.
«Геометрия для малышей» (раздел «круг»)
Воспитатель: Молодцы, хорошо сегодня занимались, я уверена, что вы теперь не спутайте круг и шар.
lit-yaz.ru
Игровое занятие для детей от 1 до 2 лет. «Круг и шар»
1. Музыкальное развитие.
Начнем наше занятие с музыкальной минутки.
Прослушиваем композицию Железновых «Игра в мяч» (ее можно найти по ссылке). Делаем движения в соответствии со словами песни:По мячу ладошкой бьём
Дружно, весело вдвоём.
Мячик — мячик, мой дружок,
Звонкий, звонкий, звонкий бок.
По мячу ладошкой бьём,
Дружно, весело вдвоём.
Мяч бросаю и ловлю,
Я с мячом играть люблю.
Мячик, мамочка, не прячь,
Мне бросай обратно мяч.
Мяч бросаю и ловлю,
Я с мячом играть люблю.
2. Коробка с мячиками – учим свойства предметов, развиваем тактильные ощущения, закрепляем понятие «большой — маленький»:
Собираем все шарообразные предметы, которые есть в доме (подойдет все, даже то, что не предназначено для детских игр: большие мячи для игры в футбол и маленькие мячики для маленьких ручек, массажные мячики, клубочки ниток, круглые фрукты: апельсины, мандарины, орехи: грецкие и лесные, настоящие воздушные шары, маленькие круглые горошинки, круглые бусины и т.п.).
ПОДСКАЗКА: если в доме не нашлось подходящего количества шариков, по аналогии можно подобрать предметы другой формы, например, кубики, машинки, коробочки и т.п. В этом случае игру можно адаптировать под соответствующий предмет.
Складываем все шарики в коробку или корзину (у нас все отлично поместилось в пластмассовую детскую ванночку).
Этап первый – изучаем свойства предметов:
Рассматриваем с ребенком все шарики и сравниваем их друг с другом, важно рассмотреть и назвать как можно больше свойств предметов, обращаем внимание на противоположные понятия: «Смотри, это большой шарик, а это совсем маленький, этот твердый, а этот мягкий, и т.п.).
Было бы хорошо, если бы Вы смогли подобрать шарики таким образом, чтобы среди них попались шарики с такими свойствами: большой, маленький, твердый, мягкий, гладкий, шершавый (шершавым и мягким, например, может быть клубок ниток или комочек из бумаги).
Этап второй – изучаем понятия «самый большой, самый маленький»:
После того как все шарики исследованы и озвучены предлагаем малышу выбрасывать по одному предметы из коробки: сначала самый большой, а за тем по убыванию размера:
— Какой шарик у нас самый большой???? Вот он! Кидай его! А теперь какой самый большой???? Вот он! Кидай его!
Не страшно если малыш самостоятельно не определит, какой из мячей будет самым большим, даже если он это сделает вместе с мамой – нужная информация у него в голове все равно отложится.
Когда все мячики выкинули из корзины, начинаем их складывать обратно. Можно продолжить игру «найди самый большой среди всех мячиков», а можно просто учиться бросать мячики с расстояния в корзину.
3.«Сюрпирзики» — развиваем мелкую моторику.
До начала занятия нужно приготовить для ребенка «сюрприз» завернуть в фольгу (а если ее нет – просто в бумагу) разные предметы.
Поскольку тема урока круги и шарики – было бы здорово, если бы мы завернули именно шарики (разные — твердые, мягкие, гладкие и т.п.). Но можно завернуть и другие предметы.
Складываем сюрпризики в ведерко, корзинку или коробочку и чем-то их накрываем (создаем элемент сюрприза). Малышу будет гораздо интереснее раскопать неизвестный клад, чем если бы ему просто предложили открыть все сюрпризы.
— Ой, смотри какая коробка! Это, наверное, зайчик нам сюрприз оставил! Что он туда положил?
Покажите как открывать сюрпризики, озвучьте предмет, который был в сюрпризе (мячик, мягкий, красный, шершавый и т.п.).
Для некоторых детей это задание может показаться достаточно сложным – все зависит от того, насколько развиты детские пальчики (и, конечно же и от того, насколько ему понравится сама игра). Перед началом игры оцените способности развития ребенка, может стоит наверх положить «сюрпризики» которые завернуты не очень плотно (их легче будет разворачивать).
4. Ищем предметы в крупе — массаж пальцев, развитие моторики, сенсорный опыт.
Положите в крупу различные предметы, покажите малышу, что в крупе кто-то спрятал клад, и предложите ему их поискать. Поскольку наше занятие тематическое – в крупу можно закопать шарообразные или круглые предметы (пуговицы, бусины, орехи). Можно вырезать кружки из картона и раскрасить их яркими цветами.
5. Аппликация – развиваем пальцы, творим, закрепляем понятие «круг», «большой-маленький», учим цвета.
В возрасте от года до двух самый простой способ обучить малыша названию цветов и фигур – это много раз озвучить название цвета и фигуры в процессе игры (красный кружок, синий кружок и т.п.).
Вырезаем кружочки разной величины и цвета. Предлагаем малышу наклеить их на бумагу в произвольном прядке. В ходе работы мы комментируем цвет каждой фигуры: «Какой красивый кружочек ты взял! Он красный, большой! И т.п.»
Либо аппликацию можно сделать сюжетной:
— Смотри, какой слоненок! Ему скучно! Давай наклеим ему веселых мячиков, чтобы он мог поиграть!
Слоненка, котенка и даже просто человечка можно также нарисовать самостоятельно.
Предлагаем выполнить любую из вариантов аппликации:
Вариант 1:
Это задание для тех, кто еще не очень хорошо знает цвета, и если вы хотите закрепить знание определенного цвета. Вырезаем из цветной бумаги кружочки двух цветов (допустим красный и синий). Предлагаем малышу наклеить кружочки на бумагу в произвольном порядке, озвучиваем: это — красный кружок ты сейчас клеишь, а это – синий.
Вариант2:
Готовим кружочки двух размеров — большой и маленький. При работе также комментируем – ты сейчас взял большой кружочек, а это маленький.
Вариант 3 – более сложный:
Вырезаем кружки и большие и маленькие и разных цветов. При наклейке озвучиваем – большой -маленький, красный, синий, большой синий, маленький красный и т.п.
Вариант 4 – самый сложный:
Еще более сложный вариант такой аппликации — попросить наклеить фигурки по просьбе:
А) простая просьба — «давай сейчас наклеим желтый кружок»;
Б) более сложная просьба — «найди и наклей большой желтый кружок».
6. Веселая зарядка — Игра на большом мяче.
Эта игра проводится на большом мяче – фитболе. Но если его нет – можно провести ее и стоя на полу – просто чуть изменив движения:
Прижимаем мяч вплотную к стене коленями так, чтобы хорошо его зафиксировать (это важно!).
Ставим малыша на мяч, держим его за обе руки, выполняем движения под стихотворение:
Давай с тобой попрыгаем, попрыгаем, попрыгаем, (прыгаем)
И ножками подрыгаем , подрыгаем, подрыгаем,
И ручками похлопаем, похлопаем, похлопаем,
И ножками потопаем, потопаем ,потопаем
Головкой покиваем
И снова поиграем
Повторяем упражнение несколько раз по кругу.
Более простой вариант стихотворения:
Девочки и мальчики прыгают, как мячики,
Ручками хлопают, ножками топают,
Глазками моргают, после отдыхают.
7. Учим предлоги.
Кладем мячик на диван, под диван, за стул, у стула. Озвучиваем свои действия малышу («смотри, я положила мячик под стул»). Можно попробовать дать малышу команду – «положи, пожалуйста, мячик под стул» (но не все дети в этом возрасте любят выполнять такие команды. Если малыш просто смотрит, как вы ставите мяч над и под – этого уже достаточно).
Для того, чтобы занятие было более игровым, мячик на стол и под стол может класть медвежонок или зайчонок (мягкая игрушка).
8. Учимся катать мяч.
Это классическое упражнение, которое развивает координацию движений. Мама и малыш садятся друг напротив друга и катают мяч друг к другу по полу.
Для этой игры можно использовать вот такие стихи:
По небу солнце ходит
И в домики заходит.
И к Тане заходит (катим мячик к малышу),
И к маме заходит (малыш катит мячик обратно),
И к Тане заходит,
И к маме заходит…
9. Расширяем словарный запас.
В завершение предлагаю прочесть вместе с ребенком замечательные стихи С. Маршака «Мой веселый звонкий мяч»Источник
upasury.livejournal.com
Чем отличаются круг от шара?
шар трехмерный, круг — 2мерный
шар — объемный. круг — плоский. <br>еще моно сказать, что шар — это множество кругов)) <br>или вращающися круг
Шар — это ПОЛНЫЙ круг!
Шар это сфера, объемная и округлая. А кругом может быть простая геометрическая фигура, начертанная где-либо, может быть определением или обстоятельством.
Шар — можно поместить только в трёхмерном пространстве…
Шар объёмен, а круг плоский
Значение круг-это круг, шар -это шар.))))
круг — фигура плоская, шар -объёмная!
шар он как 3D<br>
Тем же, чем и силиконовая грудь от ушей спаниеля
Закончи школу.Если не поможет,застрелись
Это смотря в каком пространстве ты живешь, скучно- круг, классно, интересно, восторженно — шар.
Да ни чем они не отличаются! <br>Это глупые люди придумали им разные названия. 🙂
Шару все любят, а Круга не все. (светлая ему память)
Круг — это шар, у которого отняли одно измерение.
это одно и то же, только рассматриваемое в разных плоскостях!
Круг рисуют в детском саду, А ШАР в школе …А на самом деле разница в количестве измерений.
touch.otvet.mail.ru
Калькулятор круга и шара. Рассчитать радиус, диаметр, длину окружности, площадь круга и шара, объем шара онлайн.
Калькулятор круга — это сервис, специально разработанный для расчета геометрических размеров фигур онлайн. Благодаря данному сервису Вы без проблем сможете определить любой параметр фигуры, в основе которой лежит круг. Например: Вы знаете объем шара, а необходимо получить его площадь. Нет ничего проще! Выберите соответствующий параметр, введите числовое значение и нажмите кнопку рассчитать. Сервис не только выдает результаты вычислений, но и предоставляет формулы, по которым они были сделаны. При помощи нашего сервиса вы без труда рассчитаете радиус, диаметр, длину окружности (периметр круга), площадь круга и шара, объем шара.
Вычислить радиус
Задача на вычисление значения радиуса – одна из самых распространенных. Причина тому достаточно проста, ведь зная этот параметр, вы без особого труда сможете определить значение любого другого параметра круга или шара. Наш сайт построен именно на такой схеме. Вне зависимости от того, какой вы выбрали исходный параметр, первым делом вычисляется значение радиуса и на его основе строятся все последующие вычисления. Для большей точности вычислений, сайт использует число Пи с округлением до 10-го знака после запятой.
Рассчитать диаметр
Расчет диаметра – самый простой вид расчета из тех, что умеет выполнять наш калькулятор. Получить значение диаметра совсем нетрудно и вручную, для этого совсем не надо прибегать к помощи интернета. Диаметр равен значению радиуса умноженному на 2. Диаметр – важнейший параметр круга, который чрезвычайно часто используется в повседневной жизни. Уметь его правильно рассчитать и использовать должен абсолютно каждый. Воспользовавшись возможностями нашего сайта, вы вычислите диаметр с большой точностью за доли секунды.
Узнать длину окружности
Вы даже не представляете, как много вокруг нас круглых объектов и какую важную роль они играют в нашей жизни. Умение рассчитать длину окружности необходимо всем, от рядового водителя, до ведущего инженера-проектировщика. Формула для вычисления длинны окружности очень проста: D=2Pr. Расчет можно легко провести как на листке бумаги, так и при помощи данного интернет помощника. Преимущество последнего в том, что он проиллюстрирует все вычисления рисунками. И ко всему прочему, второй способ намного быстрее.
Вычислить площадь круга
Площадь круга – как и все перечисленные перечисленные в этой статье параметры является основой современной цивилизации. Уметь рассчитать и знать площадь круга полезно всем без исключения слоям населения. Трудно представить область науки и техники, в которой не надо было бы знать, площадь круга. Формула для вычисления опять же нетрудная: S=PR2. Эта формула и наш онлайн-калькулятор помогут Вам без лишних усилий узнать площадь любого круга. Наш сайт гарантирует высокую точность вычислений и их молниеносное выполнение.
Рассчитать площадь шара
Формула для расчета площади шара ничуть не сложнее формул, описанных в предыдущих пунктах. S=4Pr2. Этот нехитрый набор букв и цифр уже многие годы дает людям возможность достаточно точно вычислять площадь шара. Где это может быть применено? Да везде! Например, вы знаете, что площадь земного шара равна 510 100 000 километров квадратных. Перечислять, где может быть применено знание этой формулы перечислять бесполезно. Слишком широка область применения формулы для вычисления площади шара.
Вычислить объем шара
Для вычисления объема шара используют формулу V=4/3(Pr3). Она была использована при создании нашего онлайн сервиса. Сайт tellaboutall.ru дает возможность рассчитать объем шара за считанные секунды, если вы Вам известен любой из следующих параметров: радиус, диаметр, длинна окружности, площадь круга или площадь шара. Так же вы можете применять его для обратного вычисления, например, чтобы зная объем шара, получить значение его радиуса или диаметра. Спасибо, что кратко ознакомились с возможностями нашего калькулятора круга. Надеемся, Вам у нас понравилось, и вы уже добавили сайт в закладки.
tellaboutall.ru
Презентация по математике «Окружность и круг. Сфера и шар»

Окружность и круг
Сфера и шар
Автор: Ноздря Алла Валерьевна
учитель математики .

На уроке :
- получите представление об окружности и круге, сфере и шаре;
- получите представление об элементах окружности и круга, сферы и шара;
- научитесь строить окружность и круг с помощью циркуля;
- научитесь измерять радиус и диаметр;
- научитесь применять полученные знания к решению практических задач.

Он не ёжик и не ёлка, У него одна иголка, Не танцор, а танцует И окружности рисует.
Циркуль – это чертежный инструмент.
На одном конце у него — игла, на другом — карандаш.
- Циркуль готов ка работе, когда иголка циркуля и карандаша находятся на одном уровне.
- Взять нужный размер, туго затянуть винт.
- При проведении окружности циркуль держи за головку.
- При работе с циркулем не оставляй циркуль в раскрытом виде, не держи циркуль вверх концами.
- Окончив работу, сложи циркуль в футляр.
1. Поставьте в тетради точку и обозначьте её буквой О.
2. Возьмите в раствор циркуля отрезок 3 см. Поставим ножку циркуля на начало линейки и разведем до обозначенной длины.
О
3. Поставив ножку циркуля с игольным наконечником в точку О, слегка наклонив циркуль, произвести круговые движения другой ножкой циркуля .
Точка О называется центром окружности
О
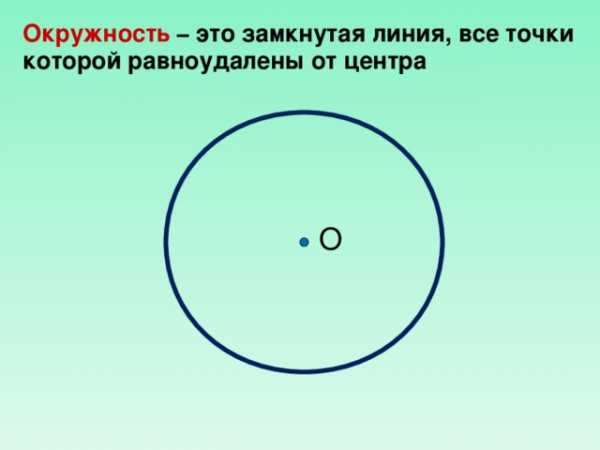
Окружность – это замкнутая линия, все точки которой равноудалены от центра
О
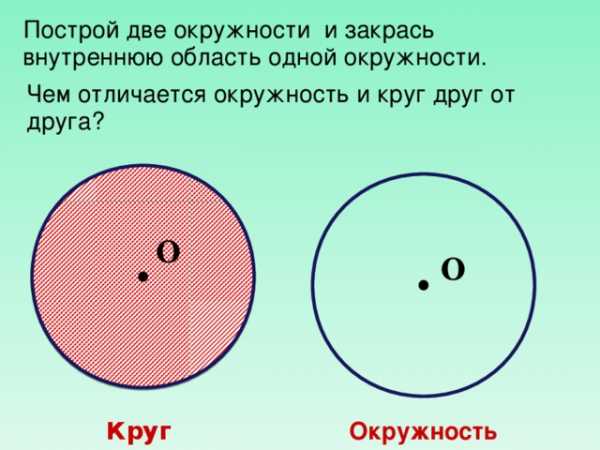
Построй две окружности и закрась внутреннюю область одной окружности.
Чем отличается окружность и круг друг от друга?
O
O
Круг
Окружность
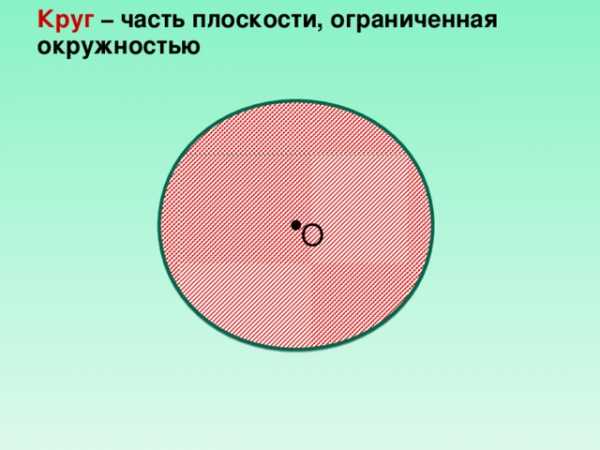
Круг – часть плоскости, ограниченная окружностью
O

O
Вот вам красный круг, кружок, По краю синий ободок. КРУГ — тарелка, колесо, ОКРУЖНОСТЬ — обруч, поясок. ОКРУЖНОСТЬ — очертанье КРУГА.
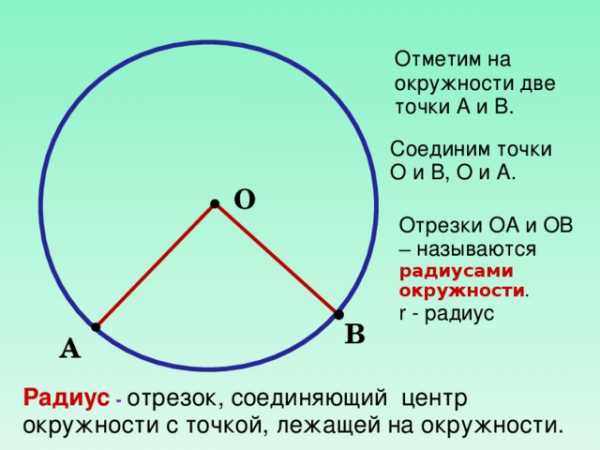
Отметим на окружности две точки А и В.
Соединим точки О и В, О и А.
О
Отрезки ОА и ОВ – называются радиусами окружности .
r — радиус
В
А
Радиус — отрезок, соединяющий центр окружности с точкой, лежащей на окружности.
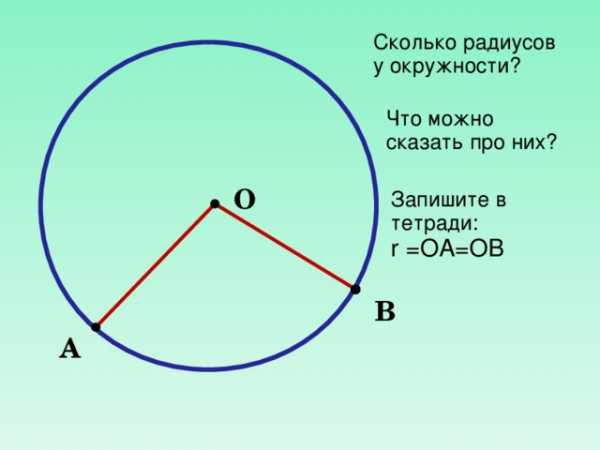
Сколько радиусов у окружности?
Что можно сказать про них?
О
Запишите в тетради:
r =ОА=ОВ
В
А
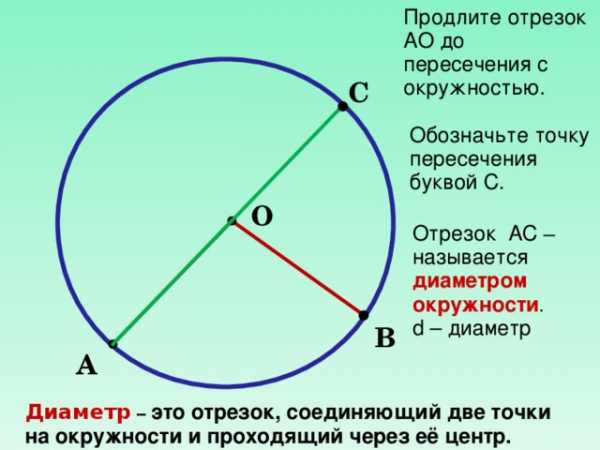
Продлите отрезок АО до пересечения с окружностью.
С
Обозначьте точку пересечения буквой С.
О
Отрезок АС – называется диаметром окружности .
d – диаметр
В
А
Диаметр – это отрезок, соединяющий две точки на окружности и проходящий через её центр.
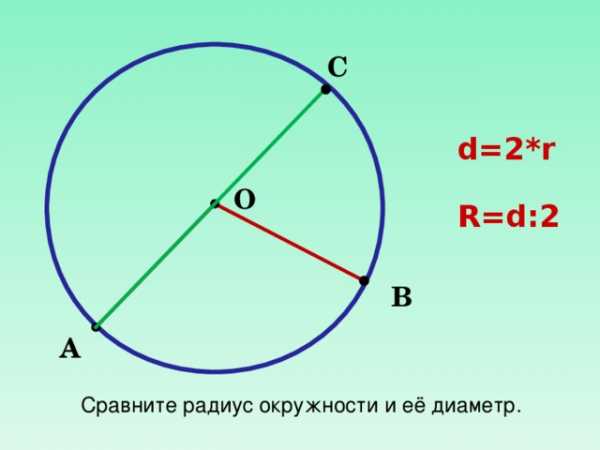
С
d=2*r
R=d:2
О
В
А
Сравните радиус окружности и её диаметр.
С
В
D
O
E
А
L
F
K
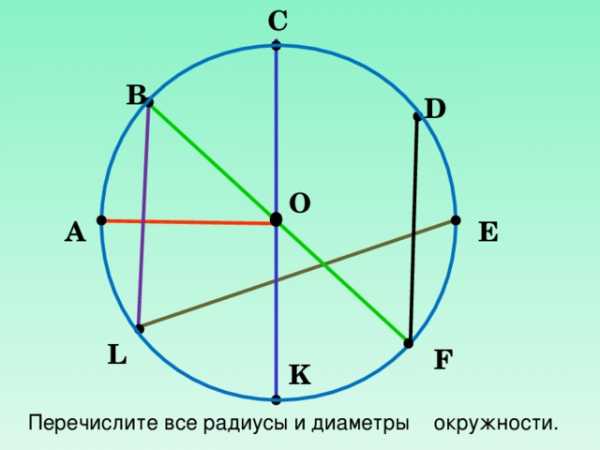
Перечислите все радиусы и диаметры окружности.
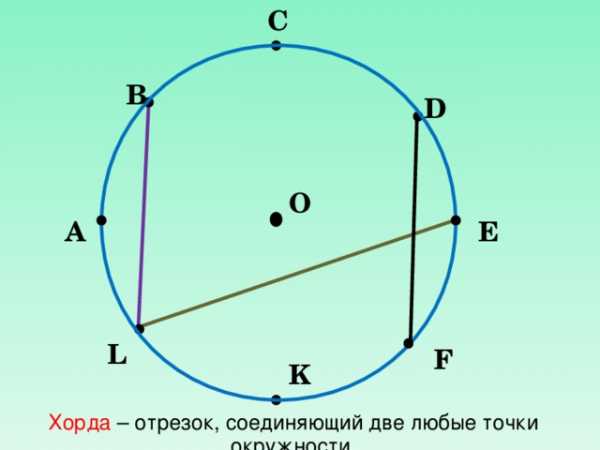
С
В
D
O
А
E
L
F
K
Хорда – отрезок, соединяющий две любые точки окружности.
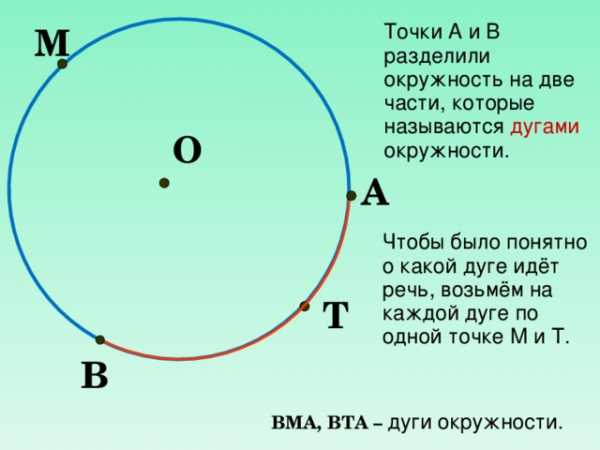
Точки А и В разделили окружность на две части, которые называются дугами окружности.
М
О
А
Чтобы было понятно о какой дуге идёт речь, возьмём на каждой дуге по одной точке М и Т.
Т
В
ВМА, ВТА – дуги окружности.
С
O
А
М
Р
K
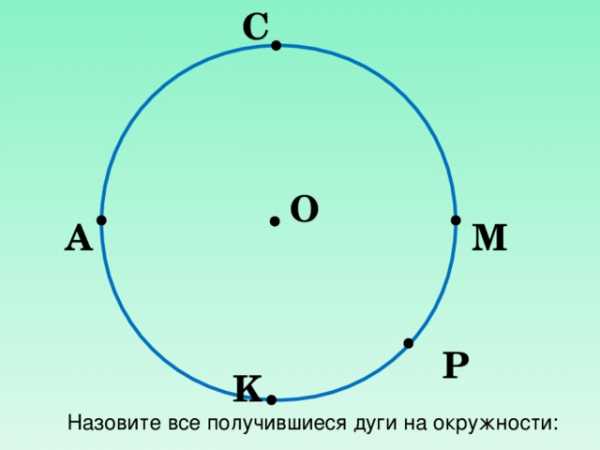
Назовите все получившиеся дуги на окружности:
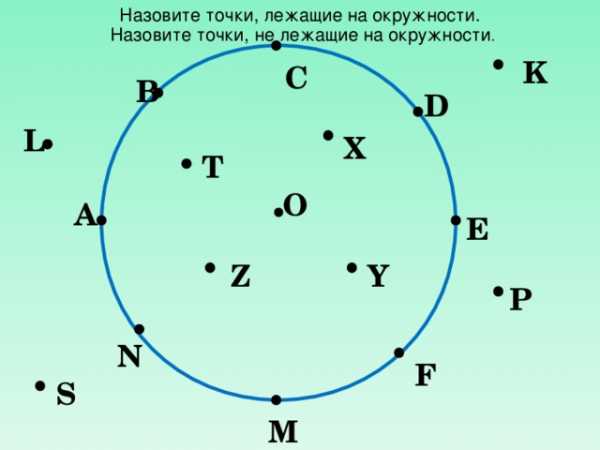
Назовите точки, лежащие на окружности.
Назовите точки, не лежащие на окружности .
K
С
В
D
L
X
T
О
А
E
Z
Y
P
N
F
S
M

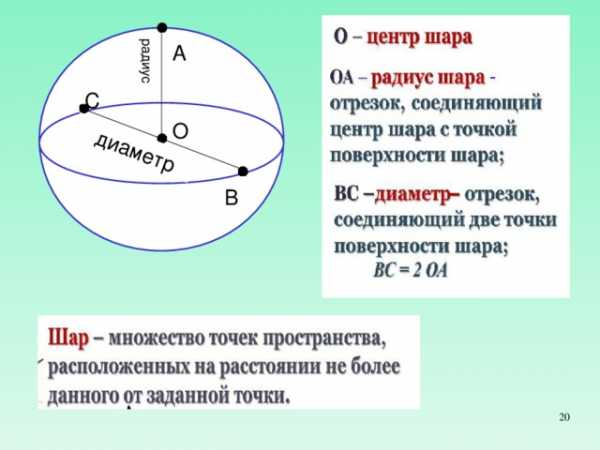
диаметр
радиус
А
С
О
В
multiurok.ru
